CNN Models

이 포스트에서는 다음과 같은 CNN Model 들과, 각 Model 에서 도입한 주요 컨셉들에 대해 살펴보겠습니다.

• 본 포스트의 내용은 coursera와 같은 온라인 강의와 다양한 블로그들을 통해 학습한 내용을 바탕으로 이해한 내용을 정리했기 때문에, 다소 부정확할 수도 있습니다. 조만간 관련 논문들을 읽고 좀더 디테일하게 정리할 예정입니다.

전통적인 CNN 모델

1. LeNet
2. AlexNet
3. VGGNet

2015년 이후의 CNN 모델

1. GoogLeNet(Inception)
2. ResNet
3. DenseNet
4. XceptionNet

LeNet

AlexNet

VGGNet

GoogLeNet(Inception)

먼저 GoogLeNet(Inception) 모델에 대해 살펴보기 전에, 먼저 1x1 Convolution 연산의 개념과 Network In Network 라는 컨셉에 대해 알아봅시다.

1x1 Convolution 연산은 말 그대로, Convolution filter 의 크기가 1x1 이라는 것을 의미하며 다음 그림과 같이 표현될 수 있습니다.

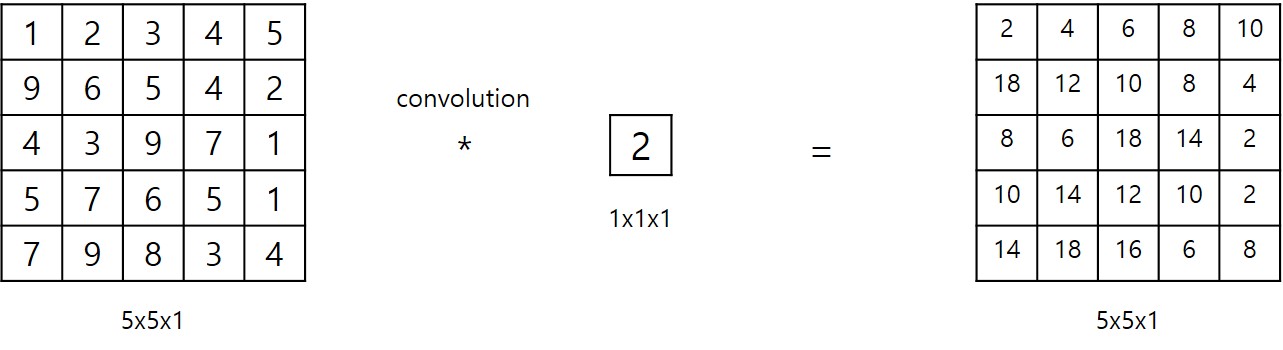
위 그림에서 보이는 것과 같이 1x1 Convolution 연산은 단순히 각각의 입력 값에 1x1, 즉 하나의 값만 곱한 결과와 같습니다.

1 Channel 을 갖는 입력에 대해 (1개의 filter 를 갖는) 1x1 Convolution 연산은 Convolution 연산에서 얻을 수 있는 이점이 전혀 없어 보입니다. 하지만 다음 그림과 같이 여러개의 Channel 을 갖는 입력에 대해 1x1 Convolution 연산을 취하게 되면 특별한 결과를 얻을 수 있습니다.

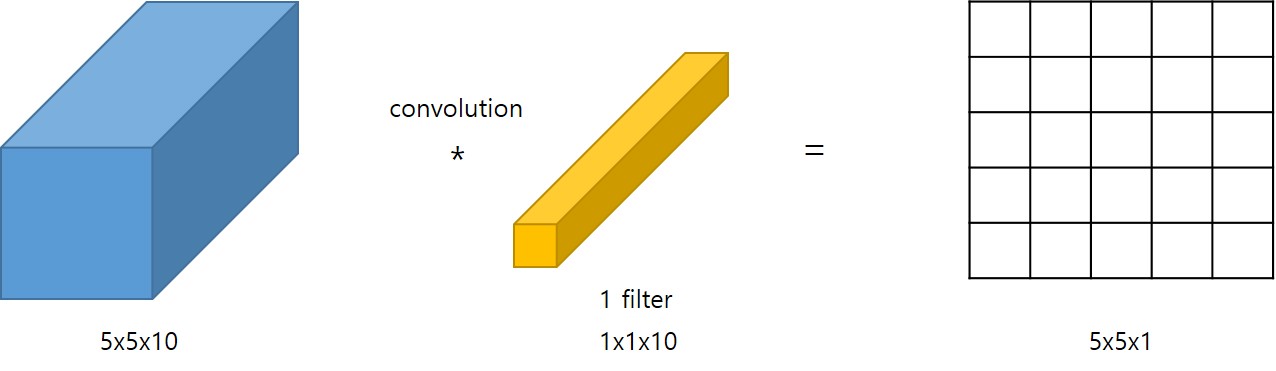
10개의 Channel 을 갖는 입력에 대해 (1개의 filter 를 갖는) 1x1 Convolution 연산을 취하면, 1개 Channel 을 갖는 결과를 얻을 수 있습니다.

여기서 주목할 점은, 1x1 Convolution 연산을 통해 출력 Channel 의 크기를 자유롭게 변경시킬 수 있다는 점입니다.

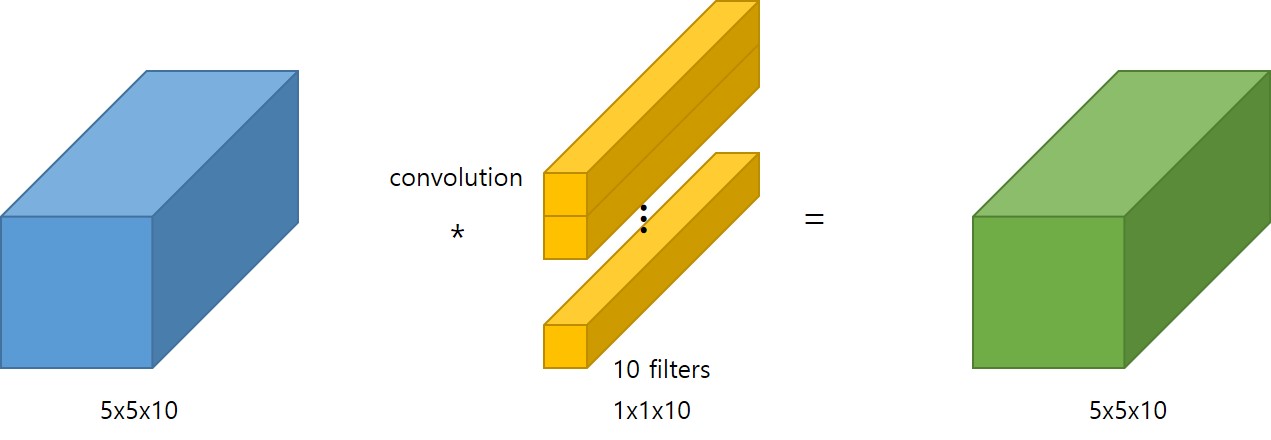
예를들어, 10개의 Channel 을 갖는 입력에 대해 10개의 filter 를 갖는 1x1 Convolution 연산을 취하게 되면, 다음 그림과 같이 10개의 Channel 을 갖는 결과를 얻을 수 있습니다.

마찬가지로 32개의 filter 를 갖는 1x1 Convolution 연산을 취하면 32개의 Channel 을 갖는 결과를 얻을 수 있습니다.

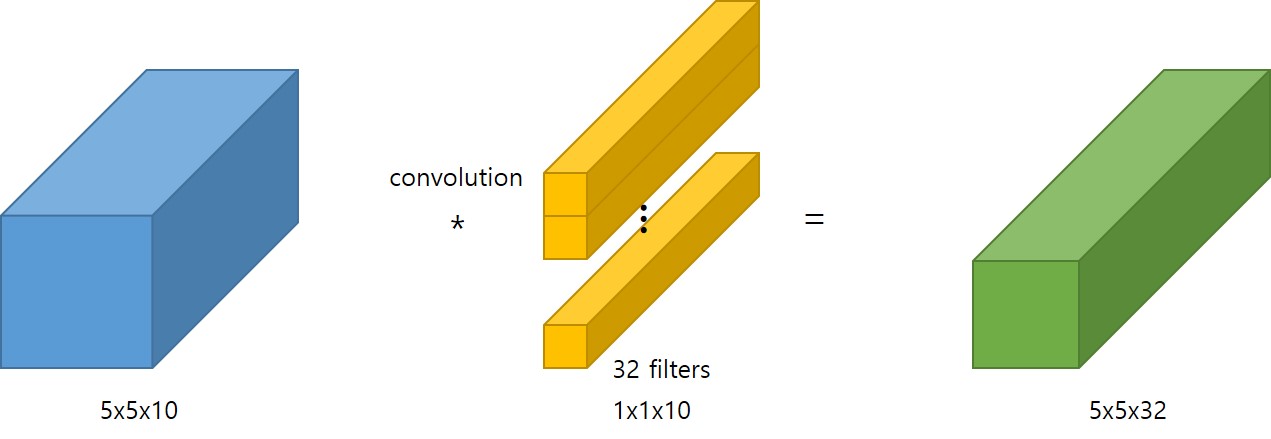
위와 같이 1x1 Convolution 연산을 취하게 되면, filter 의 개수에 따라 size 는 유지하면서 Channel 의 크기를 바꿀 수 있으며, Channel 의 크기를 작게함으로써 연산량을 크게 줄일 수 있습니다.

그렇다면 1x1 Convolution 연산과 Network In Network 라는 컨셉의 관계는 무엇일까요? Network In Network 라는 개념을 알아보기 위해 다음 그림을 살펴봅시다.

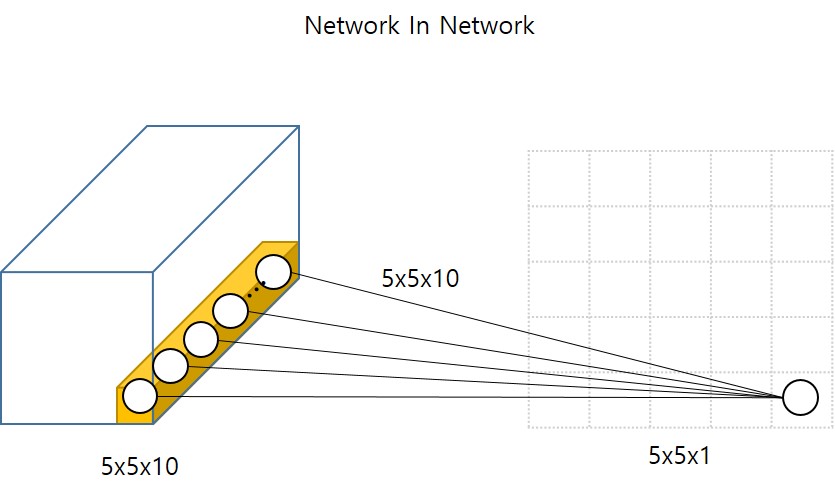
이 그림은 5x5 크기와 10개의 Channel 을 갖는 입력에 대해 1개의 filter 를 갖는 1x1 Convolution 연산을 수행하는 것을 도식화한 것입니다.

그림에서 보이는 것과 같이, 1x1 Convolution 연산은 Channel 에 대해 일반적인 Neural Network(MLP)를 수행하는 것과 유사해보입니다. 따라서 연산 관점에서(Network in) Network 를 적용했기 때문에 Network In Network 라고 부른 것 같습니다. (제가 이해하기로는…)

1x1 Convolution 연산의 또 다른 이점은 비선형성(non linearity)을 부여할 수 있다는 점입니다. 즉 비선형성을 적용하면서 원하는 크기의 Channel 의 출력을 도출할 수 있다는 점입니다. 당연히 1x1 Convolution 연산 이후 “relu”와 같은 non linear activation 함수를 적용하면 비선형성을 적용한 결과를 얻을 수 있겠죠

자, 이제 이러한 1x1 Convolution 연산에 대한 내용을 숙지하고, google 연구팀이 개발한 GoogLeNet(inception)에 대해 살펴봅시다. 이름이 GoogLeNet(inception)인 이유는, CNN 연구의 시작을 알린 LeNet에 대한 경의를 표하기 위함이라고 합니다. inception 이라는 이름은 또 다른 이름인데, inception 영화의 “We Need To Go Deeper” 라는 표현에 영감을 받아 사용했다고 하네요.

만약 CNN 모델을 디자인하고자 한다면 Convolutional Layer의 filter 크기를 1x3으로 할지, 3x3으로 할지, 5x5로 할지, 어느 시점에 어떤 크기의 pooling layer를 적용할지를 고민해야 합니다.

여기서 GoogLeNet(inception) 모델이 시도한 것은, “이것들 전부를 적용하자!” 입니다. 다음 그림은 이러한 개념을 적용한 GoogLeNet(inception) 의 inception 모듈을 개략적으로 도식화한 것입니다.

당연히 이러한 개념은 하나의 입력에 대해 다양한 크기의 filter 를 갖는 convolution 연산을 취함에 따라, 학습이 필요한 파라미터수가 크게 증가해서 연산량이 많아지는 문제가 발생합니다. 이때, 1x1 Convolution 연산을 적용해서, 먼저 입력 차원을 줄인 후, 3x3, 5x5 Convolution 연산을 수행하면 연산량을 효과적으로 줄일 수 있습니다. 다음 그림은 실제 GoogLeNet(inception)에서 사용한 inception module 을 도식화 한 것입니다.

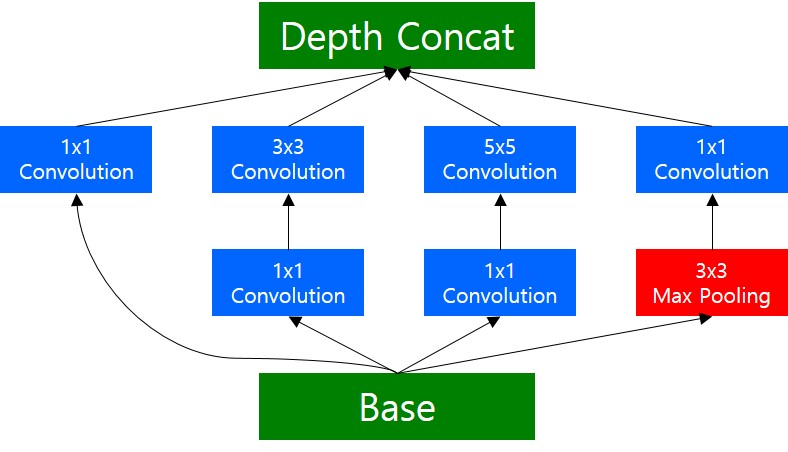
그림에서 보이는 것과 같이, 3x3, 5x5 Convolution 연산의 연산량을 줄이기 위해, 바로 전에 1x1 Conovolution 연산을 적용하여 입력 차원을 줄이고, 3x3, 5x5 Convolution 을 수행하는 것을 확인할 수 있습니다. Max Pooling 의 경우 순서가 다른데, Pooling 연산의 경우, Channel 의 크기를 변경시키지 않기 때문에, Pooling 연산을 수행한 후, 1x1 Convolution 연산을 통해 Channel(Depth) 를 맞춰주는 역할을 합니다.

이러게 정의된 inception module 들을 이어붙인것이 GoogLeNet(inception) 이며, 도식은 다음과 그림과 같습니다.

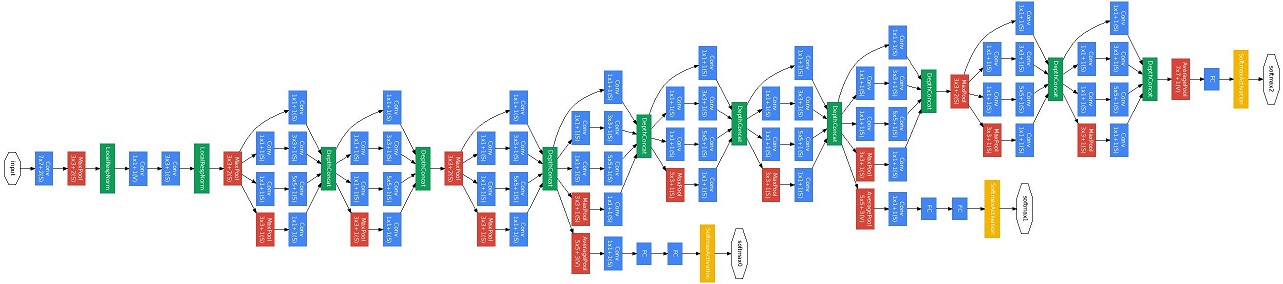
최근에는 inception_v2, inception_v3, inception_v4, inception과 resnet을 결합한 inception_resnet 등등 inception module을 기반으로 한 다양한 모델이 연구되었는데, 조만간 공부해서 정리해보겠습니다~

ResNet

ResNet 에서 도입한 가장 중요한 키 컨셉은 Skip Connection(short cut) 입니다. 기존의 CNN을 포함한 모든 Neural Network 는 네트워크가 깊어지면(히든 레이어가 많아지면) 학습 시 gradient 가 매우 작아지거나 커지는 vanishing/exploiting gradient 문제가 발생합니다. ResNet 에서는 이러한 문제를 해결하기위해 Skip Connection(short cut) 이라는 개념을 도입했는데, 한번 살펴봅시다.

먼저 Skip Connection(short cut) 이란, 몇 단계 이전 레이어에서의 출력을 현재 레이어의 출력(activation 이전)에 더하는 것을 의미합니다. 간단하게 도식화하면 다음 그림과 같이 표현할 수 있습니다.

여기서 주목할만한 점은, 이러한 Skip Connection(short cut) 이 항등 함수를 학습하기 쉽게 만들어준다는 점입니다. 예를들어, 일반적인 Neural Network 의 \(l+2\) 번째에 레이어에 대한 activation 결과를 수식으로 표현하면 다음과 같이 표현됩니다.

\[a^{[l+2]} = g(z^{[l+2]}) \\ a^{[l+2]} = g(w^{[l+2]}a^{[l+1]} + b^{[l+2]})\]

이제, Skip Connection(short cut) 을 적용해봅시다.

\[a^{[l+2]} = g(z^{[l+2]} + a^{[l]}) \\ a^{[l+2]} = g(w^{[l+2]}a^{[l+1]} + b^{[l+2]} + a^{[l]})\]

이렇게 Skip Connection(short cut) 이 적용된 수식에서, 현재 레이어(\(l+2\)) 의 weight와 bias가 0이 된다고 가정해보면, 다음과 같은 항등 함수 형태로 표현될 수 있습니다.

\[a^{[l+2]} = g(a^{[l]})\]

그 결과, 네트워크의 깊이가 깊어져도, gradient 를 최대한 유지하면서 학습시킬 수 있게 되는것 같습니다.(아직 논문을 보고 확신한게 아니라서,…)

DenseNet

XceptionNet