Paper Review - Deep Ranking

이 포스트에서는 2014년 CVPR에 실린 “Learning Fine-grained Image Similarity with Deep Ranking” 논문에 대해 살펴보겠습니다.

Key Point

• deep ranking model that can learn fine-grained image similarity model directly from images
• new bootstrapping way to generate the training data
• multi-scale network structure for captures both semantic similarity and visual similarity
• computationally efficient online triplet sampling algorithm
• publishing evaluation dataset

이미지 분류(Image Classification)와 유사 이미지 순위(Similar Image Ranking) 문제의 차이

이미지 분류에서는 “검은색 자동차”, “흰색 자동차”, “짙은 회색 자동차”는 모두 “자동차”라는 하나의 카테고리로 분류되지만, 유사 이미지에 대해 순위를 매기는 문제에서는 동일 카테고리내에서 “검은색 자동차”를 기준으로 순위를 매긴다면, “흰색 자동차”보다는 “짙은 회색” 자동차의 순위가 높게 매겨져야 합니다. 즉, 이미지 순위 문제에서는 이미지에 대한 시멘틱 유사성 뿐만 아니라 시각적 유사성도 함께 고려해야 합니다. 또한, 이미지를 특정 카테고리로 분류하는 것이 아니라 각 이미지 샘플들간의 유사성을 직접적으로 비교할 수 있는 방법이 필요합니다.

Image Similarity Model

먼저 앞서 이미지 분류와 유사 이미지 순위 문제의 차이에서 소개된 바와 같이, 이미지 순위 문제를 해결하기 위해서는 각 이미지를 특정 카테고리로 분류하는 것이 아니라, 각 이미지간의 유사성을 직접적으로 비교할 수 있는 metric이 필요합니다. 이 논문에서는 먼저 이미지간의 유사성을 비교하기 위해 triplet 이라 불리는 집합을 사용합니다. triplet 은 query image, positive image, negative image으로 구성되며, 이 때, positive image 는 negative image보다 query image와 유사성이 높도록 구성합니다. 이렇게 구성된 triplet을 이용해서 각 이미지 간의 유사성을 비교하기 위해 다음과 같은 squared Euclidean distance를 정의합니다.

\[D(f(P), f(Q)) = ||f(P)-f(Q)||^2_2\]

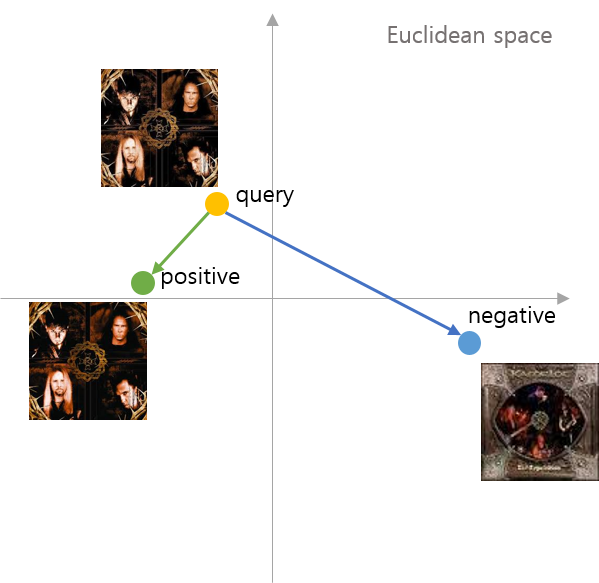
여기서 \(f\) 는 입력 이미지를 Euclidean 공간으로 맵핑하는 이미지 임베딩 함수를 의미하며, CNN과 같은 모델이 적용될 수 있습니다. 또한 \(P\)와 \(Q\)는 각각 서로 다른 이미지를 의미합니다.

이제 이와 같이 정의된 거리 함수를 이용해서 query image와 positive image, query image와 negative image간의 유사성에 대한 수식을 정의해봅시다.

\[D(f(p_i), f(p_i^+)) < D(f(p_i), f(p_i^-)) \\ \forall p_i,p_i^+, p_i^- \enspace such \enspace that \enspace r(p_i, p_i^+) > r(p_i, p_i^-)\]

여기서 \(p_i\) 는 query image, \(p_i^+\)는 positive image 그리고 \(p_i^-\) 는 negative image를 의미합니다. 당연히 이 triplet에서, query image와 positive image 사이의 거리는 query image와 negative image 사이의 거리보다 짧아져야, 상호간의 유사성이 일치할 것입니다.

이제 이를 기반으로 triplet에 대한 hinge loss 함수를 정의해봅시다.

\[l(p_i,p_i^+, p_i^-) = max\{0, g + D(f(p_i), f(p_i^+)) - D(f(p_i), f(p_i^-))\}\]

여기서 \(g\)는 두 이미지 페어간의 거리에 대한 차이를 regularize 하기 위한 gap parameter 입니다. 쉽게 말하자면 두 거리간에 약간의 마진을 더 둬서 유사 샘플간에는 더 가깝고, 비-유사 샘플간에는 좀 더 멀리 임베딩시키기 위한 파라미터입니다. 이 hinge loss를 살펴보면, query image와 positive image간의 거리가 query image와 negative 이미지보다 커지면, loss 가 증가하게 되며, 반대는 loss가 감소하게 될 것입니다.

이제 실제로 모델을 학습(최적화)시키기 위한 목적 합수를 살펴봅시다.

\[min \sum_i \xi_i + \lambda ||W||^2_2 \\ s.t. : max\{0, g + D(f(p_i), f(p_i^+)) - D(f(p_i), f(p_i^-))\} \leq \xi_i \\ \forall p_i,p_i^+, p_i^- \enspace such \enspace that \enspace r(p_i, p_i^+) > r(p_i, p_i^-)\]

여기서 \(\lambda\)는 일반화 성능을 향상시키기 위한 regularization 파라미터이고, \(W\) 는 임베딩 함수 \(f(.)\)의 파라미터를 의미합니다. 논문에서는 \(\lambda = 0.001\)로 설정했습니다.

— 수식 이해가 좀 어렵네요… ??? —

만약 위 함수의 \(\xi_i\)를 \(\xi_i = max\{0, g + D(f(p_i), f(p_i^+)) - D(f(p_i), f(p_i^-))\}\)와 같이 수정하면, 제약없는 optimization 함수로 변경할 수 있습니다(?)

이제, 앞서 정의한 hinge loss 함수와 objective 함수를 이용해서 학습(최적화)시키기 위한 모델을 정의해봅시다.

Network Architecture

이 논문에서는 다음 그림과 같이 triplet에 포함된 3개의 이미지를 3개의 동일한 deep neural network \(f(.)\)로 전달합니다.

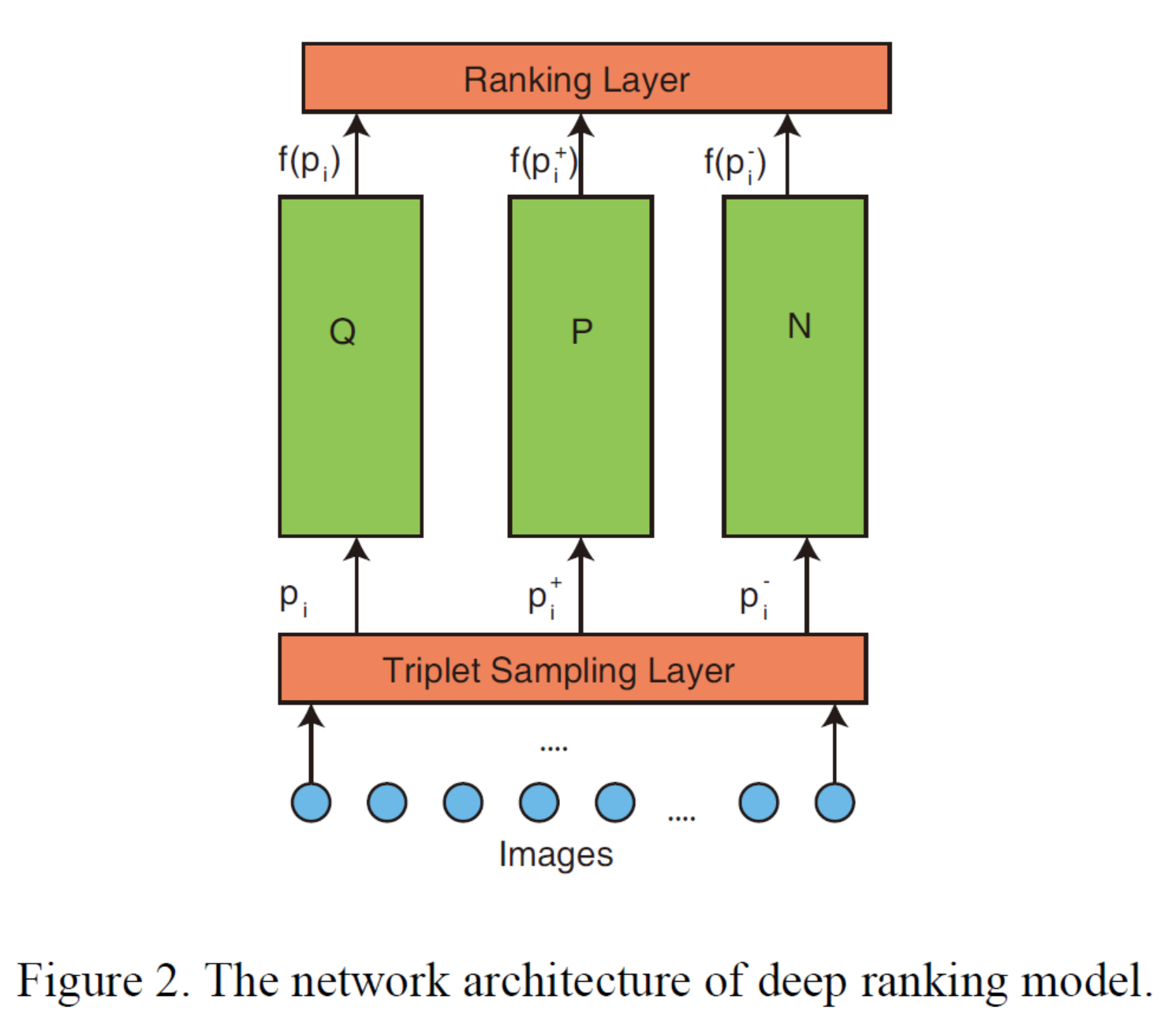
이 그림에서 표현된 deep neural network들인 Q, P, N은 각각 query image, positive image, negative image 를 입력으로 사용해서, Euclidean 공간으로 임베딩하며, 3개의 Q, P, N 네트워크들은 서로 파라미터 값들을 동일 값으로 공유합니다. 또한, 여기서 Ranking Layer는 앞서 정의한 hinge loss를 계산하는 layer로, 별도의 파라미터는 없습니다.
Triplet Sampling Layer 는 이미지 샘플들로부터 Triplet 집합을 생성하기 위한 layer로, 뒤에서 자세하게 살펴봅시다.

각각의 Q, P, N 딥러닝 네트워크들은 다음 그림과 같이 multiscale deep neural network architecture로 구성되어 있습니다.

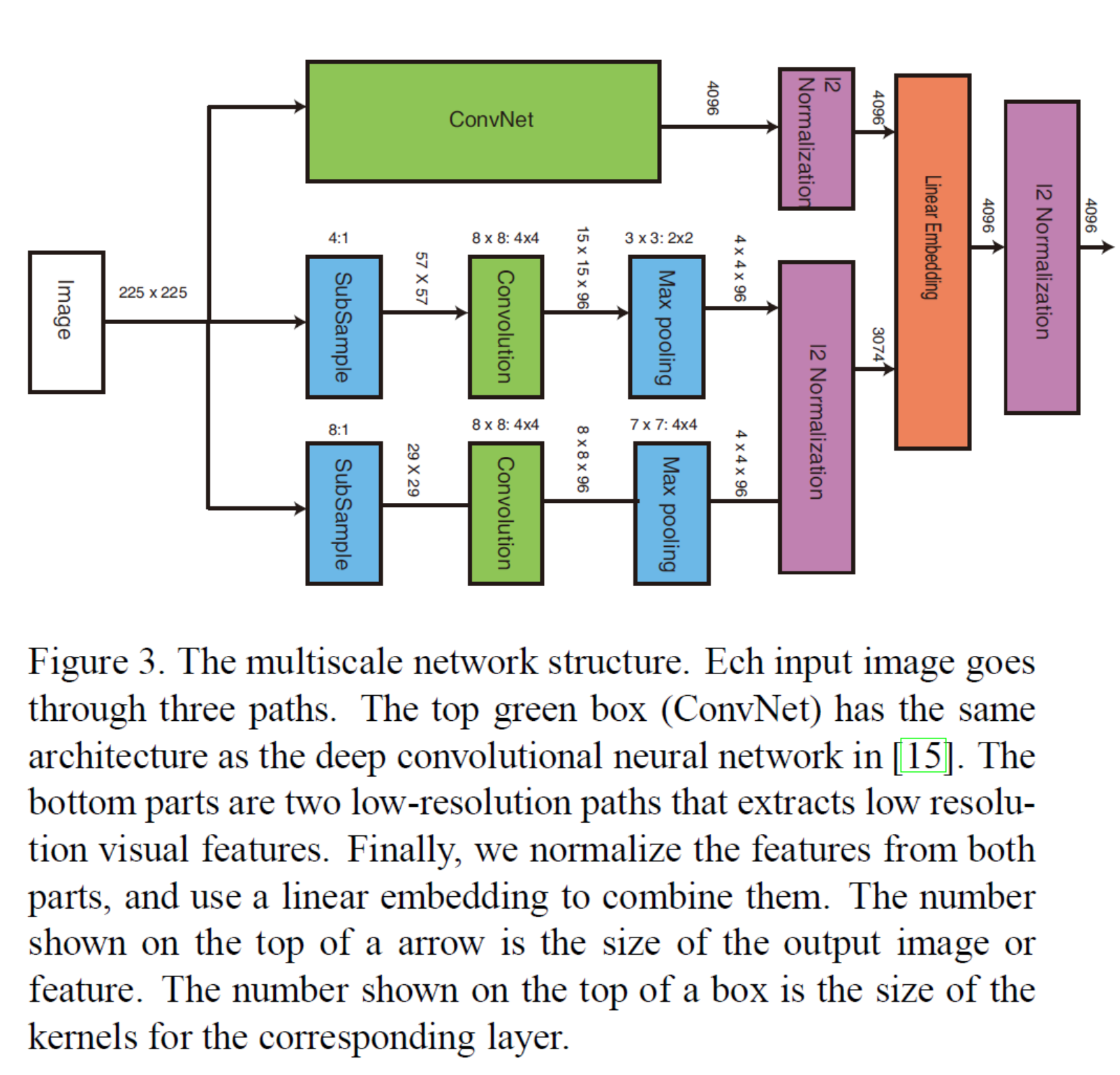
이 임베딩을 위한 딥 네트워크는 ConvNet과 상대적으로 얉은 2개의 CNN으로 총 3개의 파트로 구성되어있습니다. 여기서 ConvNet은 2012년 ImageNet 대회인 ILSVRC 2012에서 우숭한 AlexNet 모델을 그대로 사용합니다. 딥 네트워크를 위와 같이 multiscale로 구성한 이유는 semantic similarity와 visual similarity를 모두 고려하기 위해서입니다. Image Classification 문제에서 매우 효과적인 성능을 보였던 ConvNet(AlexNet)을 이용해서 semantic(category-level) similarity를 고려하고, 나머지 2개의 얉은 CNN을 이용해서 visual similarity를 고려할 수 있습니다.

Optimization

모델의 학습은 momentum algorithm 을 이용해서 최적화시켰고, 과적합을 피하기 위해서, 모든 fully connected layer에 대해 0.6% 확률로 dropout을 적용했습니다. 또한, Random pixel shift를 사용해서 데이터 확장(data augmentation)을 적용했습니다.

Triplet Sampling

딥러닝에서는 다양하고 많은 대규모의 데이터를 이용하는 것이 과적합을 피하기에 좋다는 것은 당연한 사실입니다. 그러나, 수집 및 정제한 대규모의 데이터셋에 대해 triplet을 구성할 경우 데이터는 무려 \(x^3\) 형태로 많아지게 되며, 이와같이 많아진 데이터는 학습 속도를 느리게 만들수 밖에 없습니다.

예를들어 ILSVRC 2012의 ImageNet 데이터 셋은 약 \(1.2 \times 10^7\)(12,000,000)개의 이미지로 구성되어 있는데, 이 이미지들에 대해서 triplet을 생성하게 되면, 생성 가능한 triplet의 개수는 \((1.2 \times 10^7)^3 = 1.728 \times 10^{21}\)개가 됩니다. 이렇게 과다하게 많은 데이터는 현실적으로 모델을 학습시키기 어렵게 만든다는 단점이 있습니다. 따라서 이 논문에서는 online triplet sampling 알고리즘을 제안해서 약 \(2 \times 1.2 \times 10^7\)(24,000,000)개 최적의 triplet을 샘플링했습니다.

그럼 이 논문에서 제안한 좋은 triplet을 샘플링하는 방법에 대해 살펴봅시다.

먼저 query iamge에 대해 좋은 potivie image와 negative image를 구분하기 위해, 다음 수식과 같은 total relevance score를 고려해야합니다.

\[r_i = \sum_{j:c_j=c_i,j \neq i} r_{i,j}\]

여기서 \(p_i\) 는 이미지 카테고리 \(c_i\)에 대응하는 이미지를 의미합니다. 따라서, 동일 카테고리 범주 내에서 각 이미지에 대한 전체 이미지의 총 유사도 점수(total relevance score)를 먼저 구합니다. 이후 이 총 유사도 점수 \(r_i\) 가 가장 높은 이미지 \(p_i\)를 query image로 선택합니다.

이후 선택한 query image \(p_i\)에 대응하는 positive image \(p_i^+\)를 샘플링해야합니다. positive image는 query image \(p_i\) 와 동일한 카테고리 내에서 샘플링합니다.

그런데, 유사 이미지 순위 문제에서는 동일 카테고리 내에 존재하는 이미지라고 하더라도 서로간의 유사도가 다르다는 것, 즉 visual similarity를 고려해야 된다는 것을 앞서 살펴봤었습니다. 따라서, 다음 수식과 같이 먼저 query image와 동일한 카테고리 내에서 이미지들을 샘플링한 후, query image에 대해서 샘플링 된 positive image들의 유사도(relevance score)를 구할 필요가 있습니다. 아래 수식에서 \(T_p\)는 임계값 파라미터입니다.

\[P(p_i^+) = \frac {min\{T_p, r_{i, i+}\}}{\sum_{i+}P(p_i^+)}\]

위 수식을 이용해서 positive image들의 유사도 확률 \(P(p_i^+)\)를 구하고, 구해진 유사도 확률이 가장 높은 positive image을 선택합니다.

이제 마지막으로 남은 negative image를 샘플링해야 합니다. negative image는 두 가지 type으로 정의합니다.

• out-of-class negative samples:
  이 type은 query image의 카테고리와 다른 카테고리에서 negative image를 샘플링하는 것으로, 다른 카테고리 이미지들 중에서 균일하게(랜덤으로) 샘플링합니다.

• in-class negative samples:
  이 type은 query image와 동일한 카테고리 내에서 negative image를 샘플링하는 것으로, (query image - positive image)간의 유사도보다 낮은 이미지를 샘플링해야 합니다. in-class negative sample은 positive image를 샘플링하기 위해 위 수식에서 정의했던 유사도 확률을 이용합니다. 이 때, 동일 triplet내에서 positive image와 in-class negative samples 로 구해진 negative image를 구별하기 위해 다음 수식과 같이 마진(margin)을 두어 샘플링합니다.

  \[r_{i, i+} - r_{i, i-} \geq T_r, \forall t_i = (p_i,p_i^+, p_i^-)\]

이 논문에서는 위 조건들을 만족하지 않은 triplet은 사용하지 않았습니다.

사실 위 조건들을 만족하는 triplet을 샘플링하는 것도 연산량 측면에서 쉬운 일이 아닙니다. 위의 샘플링 알고리즘은 모든 이미지 pair 들에 대해서 유사도를 계산하고 비교해서 샘플링해야 하기 때문에, 모든 이미지 데이터를 메모리에 올려서 random access를 해야 하기 때문에 컴퓨팅 리소스 측면에서도 효과적이지 못합니다. 따라서, 이 논문에서는 buffer를 도입한 효과적인 online triplet sampling 알고리즘을 제안합니다.

버퍼 생성 및 버퍼 채우기

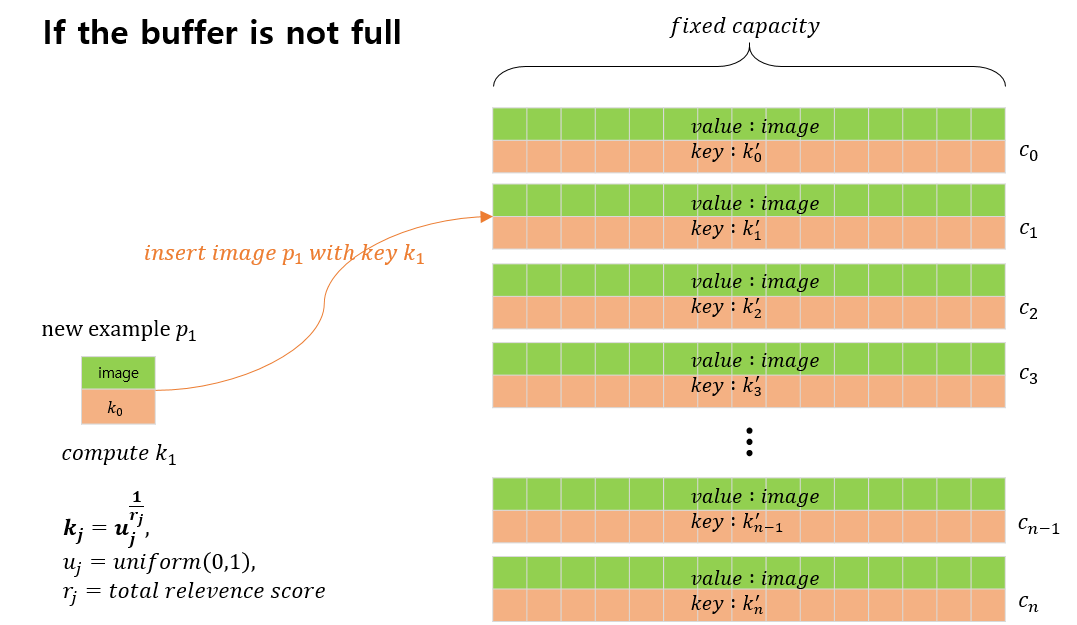
이 알고리즘에서는 먼저 위 그림과 같이 이미지 카테고리의 총 개수만큼 고정된 길이의 버퍼를 생성합니다. 이 버퍼는 각 카테고리(\(j\))별로 이미지 \(p_j'\)와 해당 이미지에 대한 key \(k_j'\) 의 두 쌍의 요소들로 구성되어 있습니다. 하나의 새로운 이미지 \(p_j\) 가 들어오면, 먼저 이미지에 대한 키값인 \(k_j\)를 구합니다. \(j\) 에 해당하는 버퍼가 모두 차있는지 아닌지 비교한 후, 모두 차있지 않으면 해당 버퍼에 이미지 \(p_j\)와 키 \(k_j\)를 추가합니다.

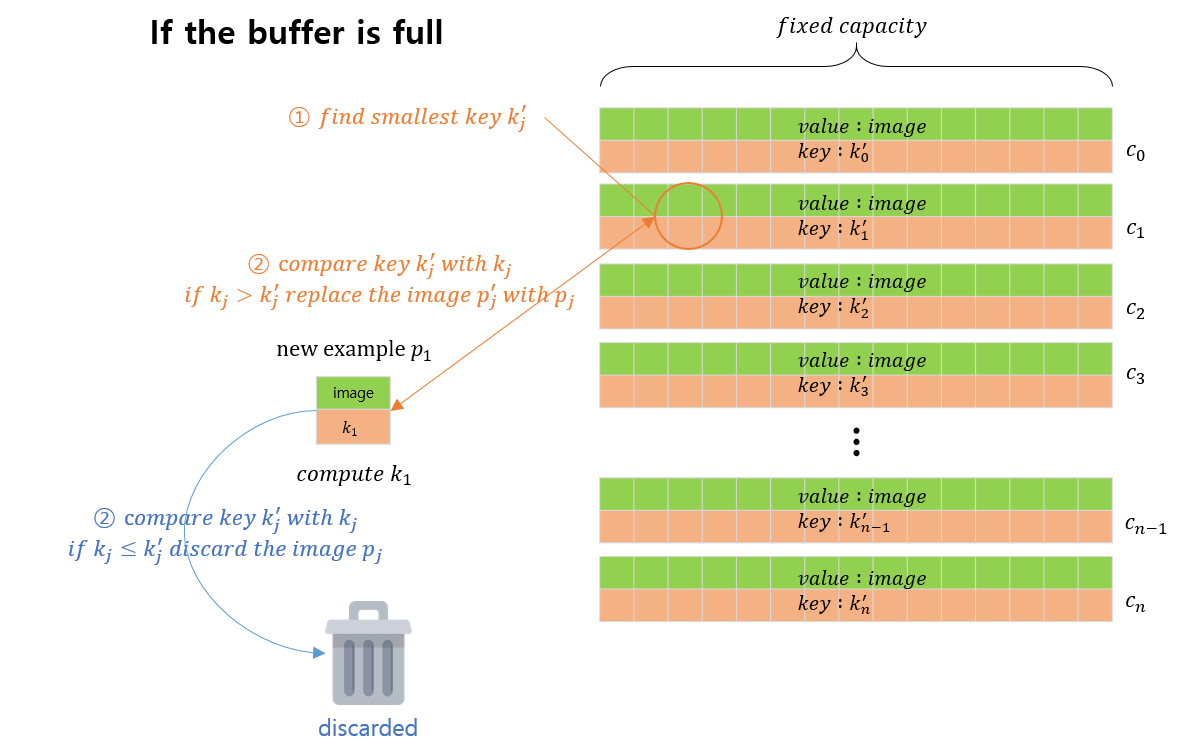
만약 해당 이미지의 카테고리 \(j\)에 해당하는 버퍼가 모두 차 있는 경우, 위 그림에서 표시되어있는 것과 같이 ①해당 버퍼의 요소들 중 가장 작은 키 값 \(k_j'\) 를 찾습니다. 이후 ② 버퍼에서 찾아낸 키 값 \(k_j'\)과 새로운 이미지에 대한 키 값 \(k_j\)를 비교합니다. 만약 \(k_j > k_j'\)일 경우, 버퍼에 포함되어있는 이미지 \(p_j'\) 를 새로운 이미지 \(p_j\)로 교체합니다. 만약 반대일 경우에는 새로운 이미지를 버리고, 새로 버퍼에 입력될 다른 새로운 이미지를 찾습니다.

버퍼에서 triplet 구성하기

이제, 구성한 버퍼로부터 유효한 triplet을 만족하는 query image, positive image, negative image를 찾아야합니다. 먼저 ①특정 카테고리 \(c_j\)에 해당하는 버퍼에 포함된 모든 이미지에서 랜덤으로(균일하게) 하나의 이미지를 찾아서 ** query image **을 샘플링합니다. ② ** positive image **의 경우, query image 와 유사하게, query image와 동일한 카테고리의 버퍼에서 랜덤으로 샘플링하는데, 샘플링된 이미지는 \(min(1, r_{i,i+}/r_{i+})\)를 만족해야 합니다. ③ ** negative image **의 경우, 앞서 살펴본 바와 같이 in-class negative image와 out-of-class negative image의 2가지 타입이 존재합니다. 먼저 in-class negative image의 경우, query image와 positive image를 샘플링할 때와 유사하게, 해당 카테고리의 버퍼로부터 랜덤으리 이미지를 샘플링하는데, 이 단계에서 샘플링된 샘플 이미지는 \(r_{i,i+}-r_{i,i-} \leq T_r\) 을 만족해야 합니다. 다른 하나인 out-of-class negative의 경우는 심플하게, query image와 다른 카테고리의 버퍼에서 랜덤하게 하나의 이미지를 샘플링하면 됩니다.

How to implement Deep Ranking Model?

// 향후 구현 예정 //

Results

// 향후 구현 예정 //

References

[1] Learning Fine-grained Image Similarity with Deep Ranking, 2014 [paper]